L'hexadécimal

Arrêter de compter!

Oui, mais mes enfants ne comptent que jusqu'à 20! Bon. Mais parti comme on est, cela pourrait coincer un peu car on a dit que le micro ne pouvait jamais s'arrêter. C'est vrai, il suffit alors de lui donner à faire une boucle infinie vide (pour l'instant, on ne l'a pas encore vu). Par contre on peut mettre un temps "infini" entre 20 et 21.

L'infini n'existe pas en informatique! Non, mais la durée que vous pouvez attendre en regardant votre carte non plus. On va mettre le temps le plus long possible. delay() attend un entier non signé long (uint32_t). Il suffit de lui donner le plus grand possible. C'est un entier sur 32 bits, c'est donc 4294967295. Comme ce n'est pas facile à écrire et surtout pour se rappeler, on va tenter une autre base.

Le nombre le plus grand sur 32 bits, écrit en binaire comporte 32 bits à 1. Au moins c'est facile à écrire sans calculatrice, quoiqu'un peu long: il suffit(!) de mettre 0b suivi de 32 chiffres 1. Il faut encore les compter!

La base 16

Le micro fonctionne avec des mots de 8 bits minimum (256 valeurs possibles). La base 10 n'est pas idéale car ce n'est pas une puissance de 2. Vous avez vu que le plus grand nombre n'est pas facile à mémoriser en décimal, alors qu'en binaire, c'est facile. Long, mais facile. Ce serait pratique de travailler en base 256, mais il nous faudrait trouver 256 chiffres différents (en base 10 on a 10 chiffres 0 à 9, en binaire on en a 2, le 0 et le 1...). C'est pour cela que l'on travaille dans une base plus petite, la base 16 ou hexadécimal. Comme il nous faut 16 chiffres et que le grand public n'en a que 10, on prendra pour compléter les lettres A ou a, B ou b, C ou c, D ou d, E ou e et F ou f. On va donc compter 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F, 10,,11,12,13... Vous avez peut être rencontré des nombres exprimés en hexadécimal, par exemple pour les adresses MAC.

On ne va pas trop s'étendre sur cette base, mais les conversions binaire hexadécimal sont simples. Si vous avez de l'hexadécimal à passer en décimal, passez par le binaire au début ou utilisez une calculatrice de programmeur comme moi (celle de windows fonctionne bien). En base 16, le chiffre le plus grand est F₁₆ qui a la valeur 15₁₀. Et pour écrire 15 en binaire, il faut 4 bits.

Pour passer de binaire à hexadécimal, on va regrouper les bits par paquets de 4. Comme en binaire on travaille sur 8, 16 ou 32 bits, il n'y aura que des paquets de 4 bits. D'ailleurs si le nombre binaire est un peu grand, on a déjà l'habitude de faire des paquets de 4, sinon c'est illisible. On fait d'ailleurs pareil en décimal en faisant des paquets de 3 chiffres. Ici, on va transformer chaque paquet de 4 bits en décimal, puis en hexadécimal (A₁₆=10₁₀, B₁₆=11₁₀, ... F₁₆=15₁₀):

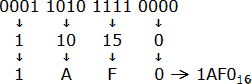
Pour passer de la base 16 au binaire, on fait l'inverse

En C on va rajouter un petit quelque chose pour différentier 1000₁₀ de 1000₁₆. Pour les nombres binaires, on rajoutait 0b devant, pour les nombres hexadécimaux, on rajoutera 0x

4294967295

C'est donc 4294967295 que l'on va exprimer en hexadécimal. C'est un nombre 32 bits donc ayant 8 paquets de 4 bits, ce qui fait 8 chiffres hexadécimaux. Le plus grand ne sera composé que du plus grand chiffre, soit F. Notre nombre c'est donc 0xFFFFFFFF. C'est finalement facile à écrire et facile à mémoriser.

Pour "arrêter" notre programme, nous allons donc exécuter l'instruction delay(0xFFFFFFFF); . Cela va donc faire une attente de 4 294 967 295 millièmes de secondes, soit presque 49 jours. Là, il faut me croire, je suis sûr que très peu d'entre vous allez vérifier.

A vous d'écrire le programme. Il ne faut pas mettre ce délai systématiquement, mais uniquement si cache arrive à 20, ou bien dépasse 20, au choix. Solution?int cacheCache; void setup() { Serial.begin(115200); } void loop() { Serial.println(cacheCache++); if (cacheCache < 10) delay(1000); else delay(300); if (cacheCache >= 20) delay(0xFFFFFFFF); }

Pour les fainéants

Une petite astuce si vous avez bien compris le binaire. En binaire le nombre non signé le plus grand ne contient que des 1, exactement comme le nombre signé -1. Si nous écrivons

delay(-1);

Le C va prendre le nombre -1 (sans doute sur 16 bits vu qu'il n'y a pas la lettre L derrière pour indiquer que c'est un long). Puis il va le passer en 32 bits car delay() attend un nombre 32 bits. On aura ainsi que des 1 en binaire. Mais comme delay veut un non signé, il interprétera notre nombre -1 comme un entier non signé. On a donc la même valeur passée que 4 milliards et des poussières. Cette façon de faire n'a aucune garantie de fonctionner dans une version future, il est possible que ceci soit "corrigé" dans un avenir.

Essayez de dire si cache est égal à 20 alors attendre avec delay(-1);. Solution?int cacheCache; void setup() { Serial.begin(115200); } void loop() { Serial.println(cacheCache++); if (cacheCache < 10) delay(1000); else delay(300); if (cacheCache >= 20) delay(-1); }

Notez bien que cette méthode n'est pas parfaite pour "arrêter" le programme car cela ne l'arrête que pour 50 jours. Mais c'est pour l'instant une alternative avec ce que nous savons. Et cela m'a permis d'introduire l'hexadécimal!