Le condensateur
Définition et unité
Un condensateur est un composant électronique à 2 bornes capable d'emmagasiner des charges électriques.
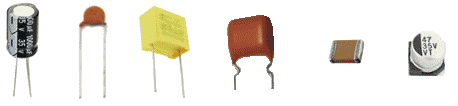
On peut imaginer un condensateur comme étant constitué de deux plaques électriques espacées d'un isolant. Si on a des charges négatives sur une des plaques, elles vont repousser les électrons sur l'autre plaque et on aura des charges positives (manque d'électrons). Les charges sont en nombre égal de chaque côté, l'ensemble est neutre. Plus on a mis de charges d'un côté, plus la tension est élevée. C'est cette idée de plaques qui a donné le symbole pour les schémas:
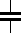
Certains condensateurs, du fait de leur réalisation sont polarisés, c'est à dire qu'une des borne doit toujours être positive par rapport à l'autre. On trouve alors différentes représentations:

La capacité d'un condensateur est son aptitude a emmagasiner plus ou moins d'énergie. C'est la caractéristique la plus importante. Elle
se mesure en farads, en abrégé: F (merci Mr Farad). C'est une unité importante et on utilise surtout les sous-multiples. Le deuxième paramètre
important est la tension maximale qui peut être appliquée. En première approche on peut classer les condensateurs en catégories:
- condensateurs céramiques et plastiques de 1nF à 1µF, non polarisés, avec des tensions de services d'au moins 100V
- condensateurs électro-chimiques ou chimique aluminium ou tantale de 1µF à 22000µF, polarisés, tension de service entre 10V et 50V
- super-condensateurs de 0,1F à 10F, polarisés, tension de service de 3,3V à 5V
Pour les condensateurs non polarisés, on ne se posera pas de problèmes quand à la tension de service.
Les condensateurs tantale ont de meilleures performances que les condensateurs aluminium, sont plus petits, mais les capacités dépassent rarement les 10µF. Les condensateurs aluminium n'ont pas une bonne tenue en haute fréquence et on voit souvent dans les montages un condensateur de 100µF en parallèle avec un condensateur plastique de 100nF. L'un est pour la réserve d'énergie pour les variations lentes, l'autre pour les rapides.
Le milli-farat est très peu utilisé et on dit plutôt 10000µF que 10mF. Sur certains condensateurs on voit parfois 1000MF; il s'agit en fait de 1000µF. Si on n'utilise ni M ni m, les lettres µ m ou M indiquent micro.
Les tolérance des aluminium de forte capacité peut être de -20%/+50%; on ne les trouve que dans la série E3 (1 2,2 4,7 et les multiples)
Les super-condensateurs sont apparus plus tard, on ne s'en sert quasiment que comme réserve d'énergie temporaire pour les mémoires ou pour avoir le temps d'arrêter les microprocesseurs en cas de coupure d'alimentation.
Il existe des condensateurs de quelques µF non polarisées qui servent de condensateur de démarrage pour des moteurs alternatifs (asynchrones monophasés).
Parallèle et série
Si on mettait deux condensateurs en parallèle, la valeur serait la somme des deux. Mais on ne le fait jamais sauf si on double un chimique avec un plastique. On a par exemple 100µF en parallèle avec 100nF. Comme expliqué plus haut ce n'est pas pour passer de 100µF à 100µF (calculs fait à 10% de précision minimum).
Si on mettait deux condensateurs de valeur C1 et C2 en série, on obtiendrait un condensateur de valeur 1 / ((1/C1) + (1/C2)). Cela permettrait de doubler la tension de service, mais dans la pratique cela ne fonctionne pas à cause des dispersions des condensateurs. A éviter.
Non discontinuité de la tension
Quand on fait rentrer des électrons d'un côté du condensateur, ces derniers ne pourront ressortir que du même côte. Et on ne peut pas les faire rentrer ou ressortir en un temps nul. On ne peut donc pas décharger un condensateur avec un temps nul, et la tension aux bornes d'un condensateur n'a pas de discontinuité. Il faut nécessairement du temps pour passer d'une tension à une autre. Si on met un condensateur en parallèle sur le 5V, ce dernier ne pourra plus tomber à 0V instantanément si on tire un fort courant. C'est la raison de leur présence sur les alimentations.
Formulaire
Je ne dis pas qu'on fait tout avec la constante de temps, mais presque. Quand un condensateur de valeur C est associé à une résistance de valeur R, la constante de temps noté τ (tau, le "t" grec) est:
τ = R C τ: constante de temps (s) R: résistance (Ω) C: capacité (F)
Quand on charge un condensateur au travers de la résistance, la montée en tension est exponentielle et au bout d'un temps τ on a 63% de la valeur finale, à 3τ on a 95% de la valeur finale. On considère alors que l'on a atteint la valeur finale (on fait souvent des calculs à 10% près), alors que pour un mathématicien, on n'atteint jamais la valeur finale.
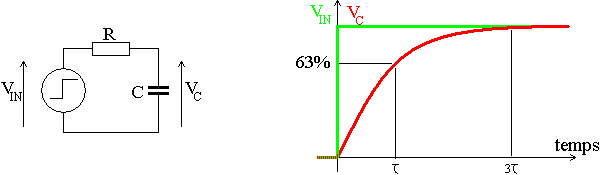
Les charges et décharges de condensateurs au travers des résistances donnent pour les tension et les courants des fonctions du type:
v(t) ou i(t) = A + B.e-t/τ
A vous de voir pour t=0 et t=∞ ce que valent les paramètres A et B. Par exemple pour la charge ci dessus sous 5V, pour t=0 on a v(0)=A+B=0 et pour t=∞ on a v(∞)=A=5V, d'ou A=5V et B=-5V et v(t)=5(1-e-t/τ).
La charge d'un condensateur noté C et exprimée en coulombs (merci Mr Coulomb) est proportionnelle à la tension et le coefficient de proportionnalité est la capacité. Et si le condensateur est chargé avec un courant constant I pendant un temps ΔT, la variation de charge est le produit I ΔT. On a donc
ΔQ = C ΔV = I ΔT ΔQ: variation de la charge (C) C: capacité (F) ΔV: variation de tension (V) I: intensité constante(A) ΔT: variation de temps (S)
La charge en coulomb n'est pas utilisée, mais la deuxième égalité est utile: si on a une alimentation qui délivre 12V sous 1A, si pendant 10ms on ne fournit plus de courant (la tension du secteur trop faible), un condensateur de 10000µF permettra de maintenir en partie la tension. Elle baissera de ΔV =IΔT/C = 1A.0,01s/0,01F = 1V . Quand la tension est maximum, on aura 12V, et au bout de 10ms, la tension sera encore de 11V. Sans condensateur, on aurait 0V
La puissance dissipée sous forme de chaleur par un condensateur est toujours nulle. Un condensateur ne peut pas chauffer. On l'utilise dans certaines alimentations 230V ou dans des ponts diviseurs (notamment en haute tension) pour chuter la tension.
En alternatif sinusoïdal, un condensateur ressemble un peu à une résistance. Quand la tension s'inverse les charges vont aussi s'inverser. Pour ce faire il va passer du courant et ce d'autant plus que l'on fait cela rapidement (d'autant plus que la fréquence est élevée). En effet, si on double la fréquence il va falloir faire passer autant d'électrons en moins de temps. On parle d'impédance (souvent notée Z) et pas de résistance car le courant et la tension ne sont pas proportionnels. Mais ce sont des histoires plus complexes. En sinusoïdal, le courant et la tension sont liés par:
1 1
U = Z I = ─── I = ──────── I
C ω C 2 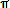 f
U: tension (V)
Z: impédance (Ω)
I: intensité (A)
C: capacité (F)
f
U: tension (V)
Z: impédance (Ω)
I: intensité (A)
C: capacité (F)
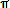 : 3,14...
f: fréquence (Hz)
ω: pulsation (rd/s)
: 3,14...
f: fréquence (Hz)
ω: pulsation (rd/s)
Enfin la dernière formule donne l'énergie stockée dans un condensateur, mais je ne crois pas que cela peut âtre utile pour développe une application Arduino:
1
W = ─ C V2
2
W: énergie (J)
C: capacité (F)
V: tension (V)
Cette formule montre que comme l'énergie stockée dans un condensateur ne peut pas changer de valeur instantanément, la tension ne le peut pas non plus. Et elle explique aussi que si on charge un condensateur de 1000µF sous 5V ou 12V et que l'on fait un court-circuit avec un fil entre les deux bornes du condensateur, on voit une étincelle: c'est toute l'énergie qui se dissipe en un instant court.
Mesure
La mesure d'un condensateur est rare. C'est un composant assez costaud, et la plupart du temps, un condensateur mort est souvent un chimique qui est bombé ou qui fuit, un liquide coulant.
Marquage
Quand le marquage ne contient pas l'unité, il s'agit de pico-farat ou de micro-farat. C'est le type de condensateur qui va guider le choix il est difficile pour une personne un peu avertie de se tromper d'un facteur 1'000'000.
Quelques condensateurs (de moins en moins) sont marqués avec des bandes de couleurs (voir marquage des résistances). Par exemple:

La première bande est en haut, bleu ⇒ 6. La deuxième ne peut pas être blanc car 60 n'est pas dans la série E12. La deuxième bande est grise ⇒ 68 (dans la série E12). La troisième bande est orange (trois zéros). La valeur est donc de 68000pf soit 68nF. Pour nous, les bandes supplémentaires (tolérance et tension) on moins d'intérêt.
Dans les autres cas, le marquage est écrit, de façon plutôt claire, ou avec 3 chiffres comme les résistances.