Matrice triangulaire

En voici le principe: avec N entrées (N>1), on va mettre systématiquement un bouton entre deux entrées quelconques. Cela donne par exemple pour 6 entrées:

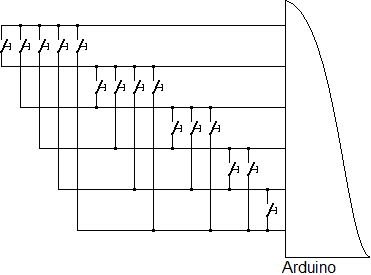
Pour lire un bouton, on commence par mettre toutes les broches en INPUT_PULLUP. On passe ensuite un côté du bouton en sortie à LOW. Si le bouton est enfoncé, l'entrée située de l'autre côté va alors passer à LOW. Pour lire l'ensemble du clavier, on passera une par une toutes les broches à LOW en lisant les autres broches. Notez que l'on doit ne faire que la moitié des lectures, par exemple si un bouton se trouve entre D₂ et D₅, on le lirait une première fois quand D₂ serait à LOW, et une seconde fois quand D₅ serait à LOW. On peut faire:
- mettre D0 à LOW et lire D₁, D₂, D₃, ... D_N
- mettre D1 à LOW et lire D₂, D₃, D₄, ... D_N
- mettre D2 à LOW et lire D₃, D₄, D₅, ... D_N
...
- mettre DN-2 à LOW et lire D_N-1, D_N
- mettre DN-1 à LOW et lire D_N

Si on numérote les entrées D₀, D₁, D₂, D₃, ... D_N, et que l'on fait un (demi) tableau pour noter le numéro des boutons possibles, cela peut donner avec 6 entrées:

On ne peut rien mettre dans la matrice sur la diagonale car on ne peut pas mettre les deux entrées d'un bouton sur la même entrée. On ne peut remplir qu'une moitié du tableau, en gris clair, on a les mêmes positions. C'est ce tableau qui va donner le nom à ce type de branchements, on ne remplit qu'une partie triangulaire de la matrice.

Pour N entrées, la matrice carrée à N² cases. En retirant la diagonale de N cases (N²-N) on a la matrice triangulaire et son image. On ne peut donc remplir que la moitié soit on peut avoir au maximum (N²-N)/2 boutons.
- avec 2 entrées: 1 bouton (vraiment aucun intérêt, pour un bouton, le mettre entre une entrée et la masse)
- avec 3 entrées: 3 boutons (n'a pas d'intérêt)
- avec 4 entrées: 6 boutons, cela commence à devenir intéressant
- avec 8 entrées: 28 boutons, à comparer avec les 16 boutons d'une matrice carrée hexadécimal classique

Si on veut un clavier téléphone 12 touches, ou un clavier hexadécimal 16 touches, on n'économise qu'une seule entrée avec la matrice triangulaire par rapport à la matrice carrée classique. Mais c'est au prix d'une complexité supplémentaire pour le décodage.

Mono?

La lecture est mono, elle fait des erreurs de lecture si deux boutons qui ont une borne commune sont appuyés. Par exemple dans le cas ci-dessus, un appui sur les boutons N°1 et N°2 met en contact les entrées D₀, D₁ et D₂, qui peut résulter d'appuis sur (N°1, N°2) ou (N°1, N°6) ou (N°2, N°6) ou (N°1, N°2, N°6). Par contre, on peut quand même savoir qu'il y a plus d'un bouton appuyé.

Algorithme simple

Voici un programme le plus simple possible montrant l'algorithme de lecture:

// Matrice triangulaire, 15 boutons sont branchés entre broches:
// (2,3), (2,4), (2,5), (2,6), (2,7), (3,4), (3,5), (3,6), (3,7), (4,5), (4,6), (4,7), (5,6), (5,7) et (6,7)

void setup()
{
  Serial.begin(115200); // Régler aussi la console à 115200 bauds!
  for (byte broche=2; broche <=7; broche++) pinMode(broche, INPUT_PULLUP); // Repos, toutes les broches en INPUT_PULLUP
}


void loop()
{
  Serial.println("\n\n(2,3) (2,4) (2,5) (2,6) (2,7) (3,4) (3,5) (3,6) (3,7) (4,5) (4,6) (4,7) (5,6) (5,7) (6,7)");
  for (byte ligne=2; ligne<=6; ligne++) // Pour toutes les lignes de la matrice sauf la dernière
  {
    digitalWrite(ligne, LOW); // Passage de la ligne en sortie à LOW
    pinMode(ligne, OUTPUT);
    for (byte colonne=ligne+1; colonne<=7; colonne++) // Pour les colonnes possibles
      if (digitalRead(colonne) == LOW) Serial.print("appui "); 
      else Serial.print("  -   ");
    pinMode(ligne, INPUT_PULLUP); // Retour au repos de la ligne
  }
  delay(500); // Pas trop souvent
}

Ce programme donne par exemple cet affichage pour un bouton appuyé entre les broches 3 et 4:

(2,3) (2,4) (2,5) (2,6) (2,7) (3,4) (3,5) (3,6) (3,7) (4,5) (4,6) (4,7) (5,6) (5,7) (6,7)
  -     -     -     -     -   appui   -     -     -     -     -     -     -     -     -   

On peut vérifier que la lecture est mono car si on presse les boutons (3,4) et (3,7) on obtient une erreur de lecture:

(2,3) (2,4) (2,5) (2,6) (2,7) (3,4) (3,5) (3,6) (3,7) (4,5) (4,6) (4,7) (5,6) (5,7) (6,7)
  -     -     -     -     -   appui   -     -   appui   -     -   appui   -     -     -   

Test si un bouton est appuyé ou non

Il n'y a pas grand chose à gagner si les broches ne sont pas sur le même port car la lecture d'une touche doit positionner deux broches avec des positions non régulières. Par contre si on place la matrice sur un port (ou sur deux si elle ne tient pas sur un seul), on peut lire plusieurs broches en même temps et cela peut aller plus vite. Dans la suite je supposerait donc que la matrice triangulaire est branchée sur les 6 bits libres du port D (broches 2 à 7 correspondant au port PD2 à PD7).

On va donc mettre une des 6 broches à LOW et lire le mot. Ce mot lu contiendra les deux bits de la liaison série ainsi qu'un 0 correspondant à la sortie que l'on a mis à LOW. Si les autres bits sont à 1, on ne voit pas de boutons appuyé. Le plus simple est de mettre alors les 3 bits qui nous gênent à 1, ainsi si le nouveau mot est à 0b11111111, aucun bouton correspondant n'est appuyé. On fera 5 fois cela pour les 5 premières broches, cela fera des doubles lectures dont on se moque.

Voici ce que cela peut donner:

// Matrice triangulaire, 15 boutons sont branchés entre broches:
// (2,3), (2,4), (2,5), (2,6), (2,7), (3,4), (3,5), (3,6), (3,7), (4,5), (4,6), (4,7), (5,6), (5,7) et (6,7)

void setup()
{
  Serial.begin(115200); // Régler aussi la console à 115200 bauds!
  for (byte broche=2; broche <=7; broche++) pinMode(broche, INPUT_PULLUP); // Repos, toutes les broches en INPUT_PULLUP
}

byte ligne; // Passage de la ligne en sortie à LOW
void loop()
{
  for (ligne=2; ligne &inf;7; ligne++) // Pour touts les lignes sauf la dernière qui n'apporte plus rien
  {
    digitalWrite(ligne, LOW); // Passage de la ligne en sortie à LOW
    pinMode(ligne, OUTPUT);
    if (((PIND | 0b00000011) | (1 << ligne)) != 0b11111111) break; // Arrêt si on a un bouton appuyé
    pinMode(ligne, INPUT_PULLUP); // Retour au repos de la ligne
  }
  if (ligne < 7) // Un bouton est appuyé
  {
    pinMode(ligne, INPUT_PULLUP); // Retour au repos de la ligne
    Serial.println("Un bouton est appuyé");
  }
  else Serial.println(); // Suppression du message car aucun bouton n'est appuyé
  delay(100); // Pas trop souvent
}

On y gagne un petit peu en temps, mais ce n'est pas formidable

Bilan

- autant de boutons que de paires d'entrées
- aucun composant supplémentaire
MAIS
- lecture mono
- algorithme plus compliqué que pour une matrice carrée
- on ne trouve pas de claviers pré-connectés ainsi
- je ne connais pas de bibliothèque pour ce genre de matrice
- pas d'interruption possible

Peu intéressant en dessous de 5 ou 6 boutons. Pour 3 boutons, il faut 3 broches. Pour 4 boutons, il faut 4 broches. Autant utiliser alors une broche par bouton qui donne un algorithme plus simple. Maintenant avec 4 broches on ne peut avoir que 6 boutons, ce que l'on peut faire avec seulement 3 broches avec le montage deux boutons par broche. Mais cela nécessite des résistances en plus. Très intéressant si on a beaucoup de boutons et une lecture mono. L'algorithme est plus simple qu'avec les matrices triples.