Accélérations
Accélération constante
Très souvent si on démarre un moteur pas à pas en l'accélérant, on choisit une accélération constante, la vitesse va ainsi croître linéairement. C'est basé sur l'idée que si le moteur a pu passer d'une vitesse nulle à une vitesse V1 en un temps T, on pourra passer de la vitesse V à V+V1 dans le même temps. C'est comme un nouveau démarrage. Mais cela me pose problème car d'une part le couple du moteur diminue si la vitesse augmente, et d'autre part on a besoin de plus d'énergie (il faudra donc plus de temps) pour passer de V à V+V1 que pour passer de 0 à V1. Il faudrait donc avoir une courbe de vitesse qui croisse plus vite au début qu'à la fin. Or la forme de cette courbe dépend de la charge. En boucle ouverte, par simplification et parce que l'on sait le calculer, on utilise quand même une accélération constante.
Petit problème pour illustrer ceci: Un homme marche à 2km/h, il pèse 50 kg et son énergie cinétique est de 1/2.M.V2 soit 100 joules.
En arrivant dans les couloirs du métro sur un tapis roulant qui va aussi à 2km/h, notre homme stoppe sa marche, et continue par conséquent à avoir
une même vitesse et une même énergie cinétique. Voyant que cela ne va pas assez vite, il se met à marcher à 2km/h. Par rapport au tapis (repère
galiléen), il passe de 0 à 2km/h et dépense 100 joules pour atteindre cette vitesse. Arrivé à la fin du tapis, un grosse dame lui barre
la route, il lui rentre dedans avec sa vitesse de 4km/h et dans le choc perd son énergie de 400 joules (1/2.M.V2 avec v=4km/h) D'où
sortent ces 200 joules supplémentaires?
Ceci pour dire que pour atteindre 2km/h il lui faut 100 joules, pour atteindre 4km/m il lui en faut 400. Il faut donc plus d'énergie pour augmenter
la vitesse de 2km/h si on a déjà une certaine vitesse que si on le fait départ arrêté.
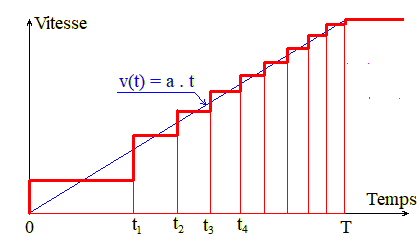
Si l'on veut quand même une accélération constante, parce que l'on ne sait pas trop quoi faire d'autre, on obtient le graphique ci-dessus. J'ai représenté en bleu la vitesse idéale. C'est une droite. Chaque palier peut être un seul pas ou plusieurs. Si il s'agit d'un pas unique, le premier palier est plus large car au fur et à mesure que la vitesse augmente, le temps pour faire un pas diminue. Si la vitesse augmente par paliers, et que l'on veut des paliers de même durée, il faut avoir peu de pas au début, ce qui n'est pas plus simple. Ici n'est représenté que 10 paliers pour une question de lisibilité. Dans la suite, je vais supposer que chaque palier n'est composé que d'un pas (ou d'un micro-pas). Bien entendu est représenté la vitesse théorique issu de la commande; dans la pratique quand on fait le premier pas, la vitesse est importante, suivi d'un arrêt, voir de quelques oscillations.
Le calcul de l'accélération, dans le cas d'une rampe de vitesse linéaire n'est pas complètement triviale si on veut faire le calcul en temps réel.
Mais on peut avoir assez facilement une idée de la vitesse qu'il faut donner au moteur.
En notant:
t le temps,
v(t) la vitesse en fonction du temps, angulaire du moteur ou linéaire de la charge,
d(t) la distance parcourue en fonction du temps, angle ou distance,
A l'accélération,
on peut écrire: v(t) = A . t soit t = v(t) / A (1)
d(t) = A . t2 / 2 (si vous dérivez la distance par rapport au temps, vous obtenez la vitesse) soit
t = √ (2 . d(t) / A) (2)
en mixant les équations (1) et (2): t = v(t) / A = √(2 . d(t) / A) soit
v(t) = √(2A) . √(d(t))
Comme la distance parcourue est proportionnelle au nombre de pas faits, la vitesse est donc proportionnelle à la racine carrée des pas faits.
Quand j'ai écrit ma bibliothèque, plutôt que demander comme paramètre l'accélération angulaire, la vitesse de rotation, j'ai préféré travailler avec les nombres de pas. Je sais par exemple que sur l'axe n°1, j'ai 800 pas par cm. Je n'ai pas à convertir la distance que je veux faire en angle. Si il faut que je convertisse ma distance en angle, je vais convertir des entiers en réels, ce qui va me faire éventuellement des arrondis et des calculs plus longs que si je travaille avec des entiers. Si je fais la somme de tous les pas que je fais, j'aurais toujours le nombre exact, alors que je ne peux rien garantir si je cumule les angles.
Dans le même esprit, je n'utilise pas le paramètre d'accélération. Mon problème pourrait être se déplacer à 10 cm/s pour aller d'un point A à un point B avec une accélération régulière sur le premier centimètre. Avec mes 800 pas/cm et un moteur de 200 pas, tout calculs faits, cela donne une accélération de 0,005 m/s2 ou encore 0,785 rd/s2 ou encore 100 pas/s2. Aucun de ces chiffres ne me parlent (je ne garanti en plus pas la valeur). Pour moi, c'est plus simple de dire "je veux une accélération sur 1cm, c'est à dire sur 800 pas".
Pour écrire le programme avec les données: accélération sur 800 pas, une vitesse finale de 8000 pas/s (10 cm/s), comme on a
v(t) = k . √(d(t)), et que pour d(t) = 800 pas, v(t) vaut 8000 pas/s, le coefficient k vaut
8000/√(800) soit 282. On a donc v(t) = 282 . √d(t)
Le premier pas est fait avec une vitesse de 282 pas/s, le deuxième à 282√2 (399 pas/s),... le 800ème à 282√800 soit
8000 pas/s .
Pour faire un décélération, il suffit de prendre le calcul dans l'autre sens, le premier pas se fera à la vitesse de 8000 pas/s, l'avant dernier à 399 pas/s, le dernier à 282 pas/s.
Accélération par paliers avec une table
Le problème pour faire une accélération linéaire telle que celle ci dessus est qu'il faut extraire une racine carrée pendant l'intervalle séparant deux pas. Or si on travaille à faible vitesse, on a bien le temps de faire le calcul, mais on n'a pas trop besoin de l'accélération car le moteur peut démarrer en direct, et si on veut passer en sur-vitesse, on n'a plus le temps de calculer la racine. Notez aussi que si on utilise les micro-pas, cela va notablement diminuer le temps de calcul disponible. Une solution classique consiste à faire des paliers de vitesses que l'on calculera à l'avance. Soit on utilise une table de vitesses, soit on utilise une table de coefficients. Ainsi le calcul n'est plus qu'une règle de trois. Pour calculer les paliers, le plus simple est que chacun aient le même nombre de pas, et on peut alors appliquer les formules ci-dessus.
Si on veut faire une accélération sur 33 paliers par exemple (le dernier palier étant la vitesse finale, ce qui fait une table de 32 valeurs), les coefficients des vitesses sont √(1/33), √(2/33) ... √(32/33). Et si on veut faire l'accélération sur 800 pas les paliers feront 800/32 = 25 pas. Si le nombre ne tombe pas juste, il y a la possibilité de faire des paliers identiques et de garder le reste pour la pleine vitesse, ou de faire quelques paliers plus long.
Accélération par la méthode de Martin
Parfois on cherche absolument à coller avec une accélération constante. Nous avons vu que ce n'est pas forcément une excellente idée, car les premiers pas sont moins contraignant que les derniers. En fait au lieu d'une courbe en racine carrée, ce serait mieux d'avoir une courbe de vitesse plus rapide au début. On peut se contenter d'une courbe approximative, de toutes façon on ne peut pas avoir la courbe optimale car elle dépend fortement du moteur et de la charge. L'idéal est en tout cas une courbe qui soit au dessus de la racine carrée, et qui soit rapide à calculer.
En fait on ne programme pas la vitesse, mais le temps qui sépare deux impulsions. Pour la programmation, on utilise soit un délai soit un timer. Dans les deux cas, c'est une unité de temps, c'est à dire l'inverse d'une vitesse. Comme nous avons vu que la vitesse devrait être proportionnelle à la racine carrée du nombre de pas parcourus, la durée de la temporisation devrait être proportionnelle à l'inverse de la racine carrée. En notant cn le temps pour le pas n (unité à définir en fonction de la programmation), on a: cn = k / √n avec n le nombre de pas ou le nombre de paliers faits.
En multipliant par √n, on obtient k = cn √n et on a donc k = cn √n = cn+1 √(n+1) k ne m'intéresse pas pour l'instant, c'est cn+1 que je cherche. Cela donne cn+1 = cn √(n/(n+1)) = cn √(1-1/(n+1)) On peut approximer √(1-1/(n+1)) par (1-1/2n). Cela va nous donner une valeur proche si n est important, et une erreur importante pour les petites valeurs. Mais on a vu que ce n'est pas très important d'avoir une valeur approximative. Notez aussi que les calculs ne seront pas fait avec une précision infinie, ce qui peut introduire des erreurs d'arrondi supplémentaires. Ce n'est donc pas la peine d'avoir une méthode de calcul exacte. Cela nous donne donc cn+1 = cn (1-1/2n) ou encore cn+1 = cn - cn/2n Cette formule est plus rapide à calculer que l'inverse d'une racine carrée.
Les formules de Martin donnant le remplacement de 1/√n sont les suivantes:
c1 = √(pi/4) soit environ 0,8862
cn+1 = cn (1-1/2n) pour les accélérations
cn = cn+1 (1+1/2n) pour les décélérations
Voyons déja pour les accélérations. Comparons là avec √n (vous pouvez utiliser un tableur par exemple):
| n | cn | 1/√n | erreur |
| 1 | 0,8862269 | 1,000000 | 11% |
| 2 | 0,6646701 | 0,707106 | 6% |
| 3 | 0,5538918 | 0,577350 | 4% |
| 4 | 0,4846553 | 0,500000 | 3% |
| 5 | 0,4361898 | 0,447213 | 2,5% |
| 6 | 0,3998406 | 0,408248 | 2% |
| 7 | 0,3712806 | 0,377964 | 1,7% |
| 8 | 0,3480755 | 0,353553 | 1,5% |
| 9 | 0,3287380 | 0,333333 | 1,4% |
| 10 | 0,3123011 | 0,316227 | 1,2% |
| 30 | 0,1818150 | 0,182574 | 0,4% |
| 100 | 0,0998750 | 0,100000 | 0,12% |
| 300 | 0,0577109 | 0,057735 | 0,04% |
| 1000 | 0,0316188 | 0,031622 | 0,012% |
| 3000 | 0,0182566 | 0,018257 | 0,004% |
Remplacer le 1/√n permet de simplifier les calculs et donne une vitesse toujours légèrement supérieure comme conseillé (si l'intervalle de temps est plus petit, la vitesse est plus grande).
Pour la décélération, le calcul "inverse" en partant de la valeur pour n=3000 donne:
|
|
On voit que pour les paramètres de décroissance, la vitesse décroît pas tout à fait assez vite. En général, ce n'est pas trop grave car le couple résistant peut aider au freinage.
Pour utiliser les coefficients pour la décroissance, c'est assez simple car on connaît le nombre de pas n que va durer la décroissance et la vitesse de départ, c'est à dire le cn.
Pour utiliser les coefficients en mode accélération, il faut calculer le premier coefficient c1. Ce calcul n'est fait qu'une seule fois et il est fait au moment ou le moteur tourne le moins vite; on a donc du temps pour le faire. Si cN est la vitesse finale qu'il faut atteindre au bout des N pas, il suffit de multiplier le coefficient c1 (0,8862269255) par cN.√N Ainsi toutes les vitesses sont multipliées par cette même valeur, en particulier la dernière valeur qui ainsi vaudra presque la bonne valeur. Il peut y avoir un léger dépassement de la vitesse (la table dit de 0,04% de dépassement pour 300 pas). On peut, si cela est vraiment dérangeant, plafonner la vitesse avec la valeur cN désirée.
Accélération par la méthode de David Austin
David Austin préconise une autre méthode qui donne des résultats plus proche de la rampe linéaire. Comme je ne pense pas que la rampe parfaitement linéaire soit la meilleure chose, je ne vois pas trop l'intérêt de ce calcul qui est plus complexe que la méthode de Martin. Pour plus de détails, voir cette méthode sur la page d'www.embedded.com
Calculs des paramètres avec une accélération constante
Les paragraphes suivant vont détailler comment calculer les différents paramètres lorsque l'on a des accélérations. Par exemple, je veux faire N pas à la vitesse maximale de V avec une accélération A, quel temps cela va me prendre? Dans tout ce paragraphe, je ne m'intéresse qu'au cas ou l'accélération est constante.
Pour ce paragraphe, je ne vais parler que de pas, mais si on est en micro-pas, remplacez le premier mot par le deuxième. Vous pouvez aussi remplacer
"pas" par degré ou millimètres. Je vais noter:
DA la distance parcourue en pas dans la phase d'accélération
DC la distance parcourue en pas dans la phase à vitesse constante
D la distance totale parcourue en pas dans les deux phases
V la vitesse maximale en pas/s
P le temps minimal d'un pas en s
A l'accélération en pas/s2
TA le temps d'accélération en s
TC le temps à vitesse constante en s
T le temps total (temps d'accélération et temps à vitesse constante) en s
v(t) la vitesse acquise au bout d'un temps t en pas/s
d(t) la distance parcourue au temps t en pas
L'origine des temps est pris au début du calcul qui nous intéresse.
Palier à vitesse constante
Intéressons nous tout d'abord à la partie ou le moteur est à vitesse constante. Les équations sont les suivantes:
V = Cte
v(t) = V (1) la vitesse est constante et vaut donc toujours V
d(t) = V.t (2) la distance est proportionnel au temps et à la vitesse
P = 1/V (3) les pas/s c'est l'inverse des s/pas
et au temps TC l'équation 2 donne DC = V.TC (4)
et on obtient en supprimant V grâce à (3): DC = TC/P (5)
Quelle distance est parcourue? DC = V.TC = TC/P
Quelle est la vitesse? V = DC/TC
Quelle est le temps entre pas? P = TC/DC
Quel temps a-t-on mis? TC = DC/V = DC.P
Phase d'accélération
Intéressons nous à la phase d'accélération uniquement. Les équations sont les suivantes:
A = Cte
v(t) = A.t (1)
d(t) = A.t2/2 (2)
P = 1/V (3)
et au temps TA l'équation 1 donne V = A.TA (4)
au temps TA l'équation 2 donne DA = A.TA2/2 (5)
en supprimant TA entre (4) et (5): DA = V2/2A (6)
en supprimant A entre (4) et (5): DA = V.TA/2 (7)
puis en remplaçant V par 1/P (équation (3)), on a en plus:
P = 1/A.TA (8)
DA = 1/2A.P2 (9)
DA = TA/2P (10)
On voit par les formules que si on exclu P ou V (P et V sont intimement liés), tout est déterminé si on fixe deux paramètres .
Suivant les deux paramètres que l'on se fixe, il faudra utiliser l'une ou l'autre formule:
Quelle distance est parcourue? DA = A.TA2/2 = V2/2A = V.TA/2 = 1/2A.P2 = TA/2P
Quel temps faut-il? TA = V/A = √(2DA/A) = 2DA/A = 1/P.A = 2P.DA
Quelle accélération prendre? A = V/TA = 2DA/TA2 = V2/2DA = 1/P.TA = 1/2DA.P2
Quelle vitesse atteint-on? V = A.TA = √(2A.DA) = 2DA/TA
Quel temps entre pas a-t-on en fin d'accélération? P = 1/A.TA = √(1/2A.DA) = TA/2DA
Phase d'accélération, puis décélération
En calculant la vitesse ainsi, c'est simple il suffit de remplacer dans les équations ci dessus DA par D/2 et TA par T/2. Cette possibilité va donner ce que je vais appeler l'accélération optimale. Si on a besoin de parcourir une certaine distance en un temps défini, cette accélération est la plus faible possible et la vitesse est aussi la plus faible.
Phase d'accélération, palier à vitesse constante, puis décélération
Je vais supposer que la décélération est la même que l'accélération. Je calcule pour l'accélération et je double cette phase.
V et P sont les vitesses constantes du palier. Les équations sont:
T = 2.TA + TC (1)
D = 2.DA + DC (2)
Les autres sont le mêmes qu'avant, mais elles ne sont pas indépendantes, on peut choisir:
V = A.TA (3)
DA = V2/2A (4)
DC = V.TC (5)
On a 5 équations, il faut éliminer TA, TC, DA, DC
(1) donne TC = T - 2.TA
(2) donne DC = D - 2.DA
En mettant tout cela dans (5), on a D - 2.DA = V(T - 2.TA) (6)
(3) donne TA = V/A (7)
en mettant (4) et (7) dans (6) on obtient D - 2.(V2/2A) = V(T - 2.(V/A))
ou encore D.A - V2 = V.T.A - 2V2
ou encore V2 - V.T.A + D.A = 0 (8)
Cette équation indique que si l'on fixe le temps et la distance, il y a une infinité de solutions pour choisir la vitesse et l'accélération. En effet si on va vite, on gagne de la distance dans le palier à vitesse constante, que l'on peut compenser par une plus faible accélération qui va réduire le temps ou l'on va vite. Le déterminant de cette équation "b2-4ac" valant T2.A2 - 42.D.A est toujours positif si l'accélération est infinie (on a plus de phase d'accélération ni de décélération, le démarrage est direct) il suffit de prendre la vitesse D/A. Par contre si on choisit une accélération trop faible (déterminant négatif, pas de solutions), on ne pourra pas aller suffisamment vite pour parcourir la distance dans le temps imparti. Intuitivement, si au bout de la moitié du temps, on est toujours en accélération et que l'on n'a pas encore fait la moitié des pas, comme pour la décélération, on parcourt la même distance dans le même temps, le compte de la distance n'y sera pas.
Pour qu'il y ait une solution, il faut que le "b2-4ac" soit positif. Si il est nul, il n'y a qu'une seule solution, et cela correspond à TC=0, et à ce que j'appelle l'accélération optimale.
Vu qu'il y a une infinité de choix si l'on fixe deux paramètres, il faut maintenant en fixer trois, et on peut avoir le quatrième. Si on choisit
A, T et D, on a pour calculer V une équation du 2ème ordre. Le déterminant de (8) vaut
T2.A2 - 4D.A, la solution est "(-b +√Δ)/2a" l'autre solution est négative. D'ailleurs
si cette solution est négative aussi, c'est que vous avez choisi une accélération trop faible ou un temps trop court ou une distance trop grande. La
solution est donc (si elle existe) V = (T.A+√(T2.A2 - 4D.A))/2. On a donc:
Quelle distance est parcourue? D = V2/A - V.T
Quel temps faut-il? T = V/A + D/V
Quelle accélération prendre? A = V2/(D-V.T)
Quelle vitesse atteint-on? V = (T.A+√(T2.A2 - 4D.A))/2
Quel temps entre pas a-t-on en fin d'accélération? P = 1/(T.A+√(T2.A2 - 4D.A))/2