Le binaire

J'ai parlé du jeu de cache-cache. Nous allons demander à l'Arduino de compter à notre place. L'avantage est qu'il ne fatigue pas et si on le laisse faire, il ne se lassera jamais. Mais dans ce chapitre, nous allons d'abord nous intéresser à la représentation des nombres, et nous compterons dans le prochain chapitre.

Des 0 et des 1

On dit que dans un ordinateur, il y a des 0 et des 1 seulement. C'est une représentation de "il y a 5V" ou "il y a 0V" (pour une Uno, certaines cartes comme la minipro travaillent en 3,3V, ce qui ne change rien). On n'a que ces deux valeurs parce que les calculs sont plus rapides avec des 1 et des 0 qu'avec d'autres représentations. Une case contenant un 0 ou un 1 est un bit (BInary elemenT). C'est la plus petite unité informatique utilisable. Avec un bit, je ne peux compter que de 0 à 1, c'est souvent insuffisant! Alors on va grouper ensemble plusieurs bits. Si j'ai 2 bits, j'ai 4 possibilités, 3 bits 8 possibilités...

Revenons un instant aux nombres décimaux que vous connaissez bien. Quand je dis 3526, c'est un nombre, 6 est le nombre d'unité (une unité vaut 1), 2 est le nombre de dizaines (une dizaine vaut 10), 5 est le nombre de centaines, 3 est le nombre de milliers. On va parler de poids des différents chiffres, comme si on devait mettre 3526g sur le plateau d'une balance; je peux mettre 6 poids de 1, 2 poids de 10... Et on voit:
- le plus petit poids c'est 1
- le poids d'après c'est la base (on est en base 10, on dira aussi décimal)
- le poids d'après c'est la base au carré (10²)
- le poids encore après c'est la base au cube (10³)...
- les chiffres valent entre 0 et la base moins 1 (soit 9 en décimal, 1 en binaire)

On va faire exactement pareil en binaire (base 2). Le premier poids (en partant de la droite) c'est 1, puis 2, puis 2² soit 4, puis 8... Je m'intéresse au nombre binaire 1011₂ (le petit 2 c'est la base et elle est toujours écrite en décimal). Pour savoir quel nombre est représenté par 1011₂, écrivons les différents poids, multiplions ces poids par les chiffres et faisons l'addition:

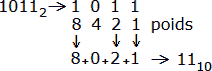
un-zéro-un-un en binaire c'est donc onze en décimal. On évitera de dire mille onze en binaire, mille ayant une signification qui n'est plus bonne.

Et les nombres négatifs?

Je donne ici une explication, mais elle n'est pas franchement utile pour faire du C. L'essentiel est la conclusion qui donne l'intervalle de représentation

Là, cela se complique un peu. En décimal on utilise un onzième symbole, le moins. En informatique on ne peut pas, car dans les cases on ne peut stocker que des 0 et des 1. On pourrait convenir que le bit de gauche du nombre serait le signe (0 positif et 1 négatif) puis que derrière on y mettrait la valeur absolue. Cette représentation existe mais elle n'est pas très utilisée. Elle n'est pas vraiment pratique, il y a en particulier 2 représentations différentes pour zéro, le plus-zéro et le moins-zéro. Vous avez certainement observé cette représentation avec certains thermomètres numérique (il y en avait dans les vieilles voitures). Et cette représentation, proche du décimal pose des questions; si j'ajoute +21 et +13, je garde le signe + et je fais l'addition 21 et 13 soit 34, le résultat est +34. Mais si je fais -21 plus +13, je vais prendre pour signe celui de la plus grande valeur et pour nombre le plus grand sans le signe moins le plus petit sans le signe: le signe est - car 21 est plus grand que 13, et le nombre derrière est 21-13 soit 8; le résultat est -8. On vient de voir que pour additionner deux nombres signés (avec un signe) il faut tantôt faire une addition, tantôt une soustraction. C'est trop compliqué.

Si on travaille sur des octets (un octet c'est 8 bits car oct- c'est 8) qui est la plus petite taille de case mémoire, on veut une représentation des nombres:
- qui ne contienne que des 0 et des 1
- comme sur 8 bits on a 256 possibilités différentes (2⁸), on veut 128 nombres négatifs et 128 nombres positifs.
- le zéro, on veut l'écrire qu'avec des zéros, et il est unique
- pour les 127 nombres strictement positifs, je veux qu'ils soit calculés comme ceux des nombres non signés
- si je veux additionner deux nombres, je les additionne comme si c'était des nombres non signés. En gros le signe sera ajouté avec la retenue de la colonne d'après et avec l'autre signe! Il en est de même pour les soustractions
- si on est sur 8 bits, on reste sur 8 bits et on calculera toujours sur 8 bits; en conséquence si cela dépasse, on ignorera la retenue qui irait s'ajouter sur la 9^ème colonne.

Pour différentier 1011 en binaire et 1011 en décimal, le C nous demande de préfixer les nombres binaires par 0b ou 0B. Ainsi onze peut s'écrire 0b1011. Les nombres décimaux n'ont pas de préfixe, 1011 est donc du décimal. Attention un nombre qui commence par le chiffre 0 suivi d'un autre chiffre est considéré comme de l'octal (base 8). On ne mettra donc jamais les zéros non significatif de gauche en décimal. Pour 0, que ce soit en octal ou en décimal, c'est la même valeur.

Pour la suite et pour bien comprendre que je travaille sur 8 bits, j'écrirais plutôt 0b00001011 (8 chiffres 0 ou 1 après le 0b).

En binaire, zéro va donc s'écrire 0b00000000.

Comment calculer l'écriture de -1? il suffit de retrancher 1 au nombre 0, pardon retrancher 0b00000001 du nombre 0b00000000. Cela semble impossible en décimal, mais en binaire on va le faire. Il faut se rappeler comment on faisait une soustraction dans une colonne. Si au milieu d'une soustraction on avait dans une colonne 2 - 5:

Faisons pareil pour 0b00000000 - 0b00000001. Pour la dernière colonne, on a 0-1. Il va falloir emprunter une deuzaine et on va avoir 10-1. C'est en binaire et en décimal cela fait 2-1 (que nous savons faire, j'espère) on va donc avoir 1 comme résultat. Pour la colonne d'après il faut rajouter le petit +1 de la colonne de droite (retenue) et on va de nouveau avoir 0-1. Cela va donc se répéter jusqu'au bout. A la fin il va y avoir dans le 9ème colonne un +1 qu'il faudrait prendre en compte. Mais on a dit que si on travaille sur 8 bits, on ignore ce qui dépasse. On va donc ignorer ce +1. Finalement -1 = 0b11111111

Une petite remarque: les 128 nombres positifs ou nuls pouvaient s'écrire sur 7 bits (car le plus grand est 127 soit 0b01111111) et le 8ème bit était toujours un zéro. Pour les 128 nombres négatifs, comme il faut prendre les autres combinaisons, le premier bit sera donc forcément à 1.

Si on regarde le poids des bits, déjà pour les nombres positifs, on a de la gauche vers la droite 128, 64, 32, 16, 8, 4, 2 et 1. Cela fonctionne. D'ailleurs comme le bit de poids fort est toujours à zéro, on peut prendre comme poids n'importe quoi, il n'est jamais dans la balance. Je vais appeler ce poids P pour l'instant. Regardons maintenant pour -1 Si on additionne tous les poids, on doit trouver -1:
P + 64 + 32 + 16 + 8 + 4 + 2 + 1 =-1
calculons P: P = -1 -(64 + 32 + 16 + 8 + 4 + 2 + 1) = -128
En binaire, pour les nombres signés, les poids sont les puissances de 2 croissantes de la droite vers la gauche, et le poids du premier bit est l'opposé de la fameuse puissance.

La question est maintenant "est-ce que cela fonctionne?" Et bien oui. mais la démonstration m'entraîne un peu loin.

Bilan des nombres signés

C'est ça qu'il faut retenir!

Si on a un nombre quelconque pour avoir l'opposé, il suffit d'inverser tous les bits et d'ajouter 1. Je ne détaille pas la démonstration, je donne juste une piste: A + /A = -1 donc A + (/A + 1) = 0 donc -A = /A + 1

Le zéro est positif, et il y a autant de nombres positifs que négatifs;

L'opposé de 0b00000000 est 0b00000000 (la retenue finale est sur le 9ème bit donc ignorée).

Sur 8 bits les nombres vont de -128 à +127. Sur 16 bits, les nombres vont de -32768 à +32767.

Sur 8 bits l'inverse de -128, si on le calcule par /A + 1 donne -128. Il y a un débordement car +128 ne peut pas exister (voir au dessus)

Sur 8 bits 128+1 donne -127. On a alors débordé.

Si une opération déborde parce que le résultat est trop grand ou trop petit, on va avoir un résultat à 256 près (sur 8 bits). Quand on compte en décimal avec autant de chiffres que l'on veut, on peut représenter les nombres sur une règle infinie:

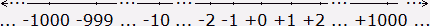
Maintenant pour les nombre binaires de l'ordinateur sur 8 bits, cela donne:

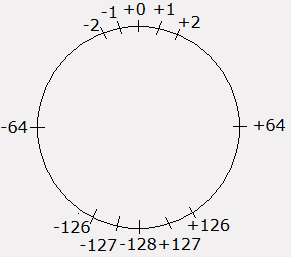
Si on n'arrête pas d'ajouter 1 on va faire des tours, et à chaque tour, il y a un débordement, on dépasse la capacité.